Page 1 of 1
The piece of mathematics with widest applicability
Posted: June 6th, 2014, 7:59 am
by Steve3007
I thought it would be interesting to see if anybody would like to propose a candidate for this prize: the piece of simple mathematics that has the widest, most diverse and useful applicability in the natural world.
There are certainly individual numbers - constants - that are interesting in this way. The Golden Ratio, pi and e, for example. But what about mathematical equations?
My inclination is to give the prize to the equations which describe Simple Harmonic Motion - sine waves and related functions. Simple Harmonic Motion (motion in which the restoring force is directly proportional to the displacement) is closely approximated in many diverse physical situations.
Anyone else care to propose any candidates?
Re: The piece of mathematics with widest applicability
Posted: June 6th, 2014, 9:26 am
by Philosophy Explorer
I would propose the process of addition. Such a process has wide applicability such as in accounting or at the cash register for example. It also implies subtraction, multiplication and division.
PhilX
Re: The piece of mathematics with widest applicability
Posted: June 7th, 2014, 9:45 am
by Keen
Normal distribution. If you take any random process and you repeat it a huge number of times, it will follow quite closely the Gaussian curve. As many things in nature are supposedly random, this simple fact is very useful when making observations.
As for non random things, I'd be tempted to choose the Cauchy Lipschitz theorem, which guarantees for instance, that the whole classical Newton mechanic is deterministic. To be a little bit more precise Cauchy Lipschitz theorem claims, that under favorable conditions (which are almost always met in nature), differential equations (like those that determine motion) have a unique solution given initial conditions.
Funny thing is that even though it is deterministic, it is still rather unpredictable, because as soon as you get too many interactions into the game, those solutions equations become impossible to calculate. If you take for instance the movement of molecules of a gas in a room, their movement is perfectly deterministic, but what happens is that there are so many forces to be taken into account that you need to treat their movement as if it was random. That is the basic idea of thermodynamics.
Re: The piece of mathematics with widest applicability
Posted: June 7th, 2014, 4:48 pm
by Steve3007
PhilX:
Yes, I can't deny that addition is profoundly important but can't really bring myself to award it the prize because there doesn't seem to be much philosophical mileage in considering why it's important. It seems too fundamental to all of mathematics. Seems too close to simply awarding the prize to the whole of mathematics.
Keen:
I very much like your contribution of the Gaussian distribution. As you've said, very widely applicable. I think that's a good candidate for the prize.
I don't know much about the Cauchy Lipschitz theorum. Looks very interesting. I'll have to do some research on it.
On the Laws of Thermodynamics and Statistical Mechanics: It's interesting that this statistical approach to modeling molecule movements that are regarded, for the purposes of the model, as random actually yields some of the most rock-solid reliable laws of physics.
As you've said, we have (at least in classical thermodynamics, as opposed to statistical mechanics) a deterministic, "clockwork" Newtonian world of little billiard-ball-like objects bouncing around off each other. It's too complex to model exactly, so it is modeled as the the statistical averaging of events that are approximated to be random, and the result, with sufficiently large numbers of molecules, is, to a very high degree of precision, deterministic again. From determinism, through randomness, back to (almost) determinism. And the single mathematical object which embodies more than any other the emergence of deterministic certainty from large collections of random events: The Gaussian!
A molecule bounces off another molecule in a deterministic and, crucially, time-reversible, way. A slight difference in the angle of collision results in a slight difference of trajectory after that collision resulting in that molecule hitting the next molecule at a different angle than it would otherwise have done. This results in a bigger difference in trajectory than for the first collision ... and so on. To determine the exact locations of all the molecules after even a fairly short space of time, even in this classical Heisenberg-free world, would require a precision of knowledge of their initial positions and velocities so great as to make their behaviour random in just as deep a sense as the randomness of Quantum Mechanics.
This exquisite dependence on initial conditions sometimes results in chaotic, fundamentally unpredictable behaviour - like the behaviour of a chaotic pendulum or the weather. But it also results in behaviour that, on a large scale, statistically, is extremely reliable and predictable, and from which the arrow of time and the concept of time-irreversible processes emerges.
It's a subject that's been discussed many times on these forums, but I'm glad you bring it up again. For the philosophy of science, it's one of the classics.
Re: The piece of mathematics with widest applicability
Posted: June 24th, 2014, 10:24 am
by enegue
I think I'll go with PE and nominate ADDITION/SUM for the award. Besides being the mathematical operation from which the others are derived, it is also fundamental to boolean algebra, where A+B represents the UNION of set A and set B.
WIth regard to the Normal distribution, it wouldn't be possible without values for the mean and standard deviation, both of which require addition to obtain, and those with a mathematical background will recognise the importance of
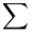
for SERIES SUMS, and

for integration (SUM of infinitesimal increments)
Philosophically, the notion of ADDITION as a UNION leads to the fundamental difference between living and non-living things. Non-living things are energised/powered by SEPARATION, e.g. lift an object (separate it from the Earth) and you increase its potential. Living things are energised/powered by UNION. e.g. the UNION of male and female gametes, sexually (animals) or asexually (plants), sets in motion the awesome process of replication and NEW LIFE (the UNION of cells).
Sociologically, the potential of a community is increased by the UNION of vision and effort of its citizens.
No doubts at all, ADDITION (aka SUM, aka UNION) should most definitely receive the award.
Cheers,
enegue
Re: The piece of mathematics with widest applicability
Posted: June 24th, 2014, 11:12 am
by Misty
COUNTING. It is the first math taught and is the basis for all math. It gives rise to the thought of order. (Like the alphabet is the basis of all words)
Re: The piece of mathematics with widest applicability
Posted: June 24th, 2014, 12:13 pm
by Present awareness
Mathematics is an abstract concept of assigning names (called numbers) such as one or two, to a quantity. It is useful in predicting an outcome within it's rules, such as 1+1=2 or 2+2=4.
Computers can make fantastic calculations with just two numbers, 0=zero for off and 1=one for on. I would say that this simple two number ratio, has the widest applicability.
Formulas for calculating the area of a circle or triangle are also very useful, and the forums E=MC2 had a huge influence on our understanding of the universe.
Re: The piece of mathematics with widest applicability
Posted: July 22nd, 2014, 7:38 am
by TimBandTech
Philosophy Explorer wrote:I would propose the process of addition. Such a process has wide applicability such as in accounting or at the cash register for example. It also implies subtraction, multiplication and division.
PhilX
I second addition, and I think Misty's counting fits in here since counting is the concept of adding one. Other words for addition are summation and superposition. Addition is what forms the calculus integral. Vector behavior is defined by the addition operator. The relativity of spatial positions is nearby. The means by which we mathematically represent geometrical space relies upon addition, as does the number itself. We exist in a state of superposition with the objects about us.
Re: The piece of mathematics with widest applicability
Posted: August 17th, 2014, 12:34 pm
by Alan Masterman
Evidently, this would have to be something of axiomatic or near-axiomatic status. The most obvious immediate candidate would be the Parallel Postulate, which made the Industrial Revolution possible.
But I am inclined to propose the logical "principle of transitivity", that is, the axiom that if A=B, and B=C, then A=C.
This is the axiom which makes measurement possible, since A = the object to be measured, B = the ruler (or other measuring device), and C = the criterion for the unit of measurement (eg the platinum metre in Paris).
-- Updated Wed Aug 20, 2014 9:15 am to add the following --
Or how about the theorem: 1+1 = 1+S(0) = S(1+0) = S(1) = 2, which is reasonably widely applicable?
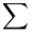 for SERIES SUMS, and
for SERIES SUMS, and  for integration (SUM of infinitesimal increments)
for integration (SUM of infinitesimal increments)